A aerodinâmica é o estudo do movimentode fluidos gasosos, relativos às suas propriedades e características, e às forças que exercem em corpos sólidos neles imersos.De uma forma geral, a aerodinâmica, como ciência específica, só passou a ganhar importância industrial com o surgimento dos aviões e dos automóveis pois estes precisavam se locomover tendo o menor atrito possível com o ar pois assim seriam mais rápidos e gastariam menos combustível.
Toda aeronave mais pesada que o ar, seja um planador ou um avião a jato, depende da aplicação da energia mecânica ao ar circundante, de forma a receber um impulso para cima, sustentando-a contra as forças de gravidade. Para que a nave se mantenha no alto, é necessária uma entrada contínua de energia, que proporcione o movimento para a frente, contra a resistência do ar. As hélices, jatos ou foguetes, fornecem o impulso necessário não só à permanência no ar, como também à subida do aparelho ou decolagem. Basicamente, um avião é composto de uma fuselagem em forma de charuto, para transportar a tripulação, a carga e os passageiros, um par de asas, localizado mais ou menos no meio da estrutura, e uma empenagem traseira, formada por um plano horizontal e um leme de direção vertical. Além disso, há um ou mais motores, montados praticamente em qualquer lugar do avião, desde o interior da fuselagem propriamente dita, até as pontas das asas. Nesse tipo de avião, a sustentação se concentra geralmente nas asas; assim, o centro de sustentação destas corresponde, normalmente, ao centro de gravidade do avião.
Várias coisas influem na aerodinâmica de um avião são elas: Peso, Sustentação, Arrasto e Empuxo.
Peso
O peso uma força que é sempre dirigida para o centro da terra: trata-se da força da gravidade. A magnitude desta força depende de todas as partes do avião, mais a quantidade de combustível, mais toda a carga (pessoas, bagagens, etc.). O peso é gerado por todo o avião. Mas nós podemos simplesmente imaginá-la como se atuasse num único ponto, chamado centro de gravidade. Em voo, o avião gira sobre o centro de gravidade, e o sentido da força do peso dirige-se sempre para o centro da terra. Durante um vôo, o peso do avião muda constantemente à medida que o avião consome combustível. A distribuição do peso e do centro de gravidade pode também mudar, e por isso o piloto deve constantemente ajustar os controles, ou transferir o combustível entre os depósitos, para manter o avião equilibrado.
Sustentação
Para fazer um avião voar, deve ser gerada uma força para compensar o peso. Esta força é chamada sustentação e é gerada pelo movimento do avião através do ar. A sustentação é uma força aerodinâmica ("aero" significa ar, e " dinâmica" significa movimento). A sustentação é perpendicular (em ângulo reto) ao sentido do vôo. Tal como acontece com o peso, cada parte do avião contribui para uma única força de sustentação, mas a maior parte da sustentação do avião é gerada pelas asas. A sustentação do avião funciona como se atuasse num único ponto, chamado centro de pressão. O centro de pressão é definido tal como o centro de gravidade, mas usando a distribuição da pressão em torno de toda a aeronave, em lugar da distribuição do peso. Além do centro de pressão, outro ponto no aerofólio é de grande importância no projeto de uma aeronave: o centro aerodinâmico. Neste, o coeficiente de momento não varia quando variamos o ângulo de ataque. O coeficiente de momento é um coeficiente adimensional que qualifica e quantifica se, para certo aerofólio, há um momento picante ou cabrante sobre o engaste da asa. Este momento é fundamental, por exemplo, na determinação das cargas aerodinâmicas para definição da estrutura e para o projeto de sistemas de controle, como o profundor.
Arrasto
À medida que o avião se move através do ar, há uma outra força aerodinâmica presente. O ar resiste ao movimento do avião, e esta força de resistência é denominada arrasto (ou atrito). Tal como a sustentação, há muitos fatores que afetam a magnitude da força de arrasto, como a forma do avião, a viscosidade do ar e a velocidade. E tal como acontece com a sustentação, consideram-se usualmente todos os componentes individuais como se estivessem agregados num único valor de arrasto de todo o avião. O sentido da força de arrasto é sempre oposto ao sentido do vôo, e o arrasto atua através do centro de pressão.Quando um avião aumenta o ângulo de ataque, aumenta também a sustentação; mas há uma geração de gradientes de pressão adversos. À partir de um certo ângulo de ataque, estes gradientes de pressão adversos resultam no descolamento da camada limite, cuja geração de vórtices de von Kárman caracteriza o fenômeno conhecido como estol. No estol, perde-se sustentação, e o arrasto aumenta significantemente. É por este fato que, na fase de decolagem de um aeromodelo, não se deve fazê-lo subir em ângulo muito acentuado. Algumas aeronaves, principalmente aquelas com projeto de calda em T, correm o risco de sofrerem "deep stall" (estol profundo), pois a esteira gerada na asa durante o estol cobre o estabilizador horizontal, fazendo-a perder capacidade de controle e impedindo que a aeronave retorne para sua atitude inicial. Por este motivo, além disso, aeronaves acrobáticas devem possuir um projeto de empenagem que garanta a saída do estol e parafuso. Aeronaves com sistemas de controle mais complexos, como os caças e jatos comerciais, em geral possuem sistemas automáticos para proteção de estol, como o "shaker" e o "pusher".
Empuxo
Para superar o arrasto, a maioria de aviões tem algum tipo de propulsão para gerar uma força chamada empuxo. A intensidade da força de empuxo depende de muitos fatores associados com o sistema de propulsão:
O tipo de motor;
O número de motores;
O ajuste da aceleração;
A hélice
A velocidade.
O sentido da força de empuxo depende de como os motores estão colocados no avião. Na figura mostrada acima, dois motores a jacto estão posicionados sob as asas, paralelos à fuselagem, com a força atuando ao longo da linha central da aeronave. Em alguns aviões (tal como o Harrier) o sentido do impulso pode ser orientado para ajudar o avião a descolar numa distância muito curta. Para os motores de jacto, pode parecer confuso considerar que a pressão do avião é uma reação ao gás quente que se escapa da turbina. O gás quente é expelido pela parte traseira, originando uma força de reação em sentido contrário: o empuxo. Esta ação-reação é explicada pela terceira lei do movimento formulada por Newton.Os motores mais conhecidos são os motores de explosão (Ciclo Otto) e os motores a jato (Ciclo Brayton). Mas também se utilizam motores elétricos e motores de foguete. Os motores elétricos e de explosão atuam usualmente por intermédio de hélices. Os motores a jacto e de foguete atuam pela força da reação.Um planador é um tipo especial de avião que não tem nenhum motor. Alguma fonte externa da potência tem que ser aplicada para iniciar o movimento. Os aviões de papel são um exemplo óbvio, mas há muitos outros tipos de planadores. Alguns planadores são pilotados e rebocados para o alto por um outro avião, e a seguir são deixados livres para deslizar em distâncias longas antes de aterrar. Uma vez no alto, a energia cinética é responsável pelo impulso, mas ela para se manter gasta energia potencial. No entanto os planadores recorrem também a uma outra fonte de energia disponibilizada pela natureza: as correntes de ar ascendente que fazem o planador ou avião ganhar energia potencial sem perda de energia cinética e assim se manterem mais tempo no ar sem uso de motores.
quinta-feira, 4 de junho de 2009
Divisão de polinômios
Ao contrário da mutiplicação na divisão de polinômios nós mantemos a base e SUBTRAÍMOS os expoentes. Por exemplo:
x³: x² = x
Pois.... 3-2 = 1 que por sua vez fica implícito
Porém existem também outras situações... Tais como:
( x²+x³- x) : x³
Façamos a situação acima passo á passo :
x² : x³= x-¹
pois 2-3= -1
x³ - x³= x° que por sua vez é nulo... então podemos, na linguagem popular, cortar este termo de nossa operação
x¹ - x ³ = x-²
Assim obtemos o resultado: x-¹ - x-2 = x-³
x³: x² = x
Pois.... 3-2 = 1 que por sua vez fica implícito
Porém existem também outras situações... Tais como:
( x²+x³- x) : x³
Façamos a situação acima passo á passo :
x² : x³= x-¹
pois 2-3= -1
x³ - x³= x° que por sua vez é nulo... então podemos, na linguagem popular, cortar este termo de nossa operação
x¹ - x ³ = x-²
Assim obtemos o resultado: x-¹ - x-2 = x-³
quinta-feira, 28 de maio de 2009
Raiz Quadrada
Matematicamente, a raiz quadrada de um número real não negativo x é o número real não negativo que, quando multiplicado por si próprio, iguala x. A raiz quadrada de x é simbolizada por √x.
Por exemplo:
porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadraticas (equações do 2º grau). A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos.
Por exemplo:
porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadraticas (equações do 2º grau). A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos.
Volume
Volume de algo é a quantidade de espaço ocupado por este, como por exemplo: uma caixa de sapato, o ar que está dentro é o volume dela, ou se enchermos um copo de água, a quantidade de água que comporta seria o volume.
Para caucular o volume devemos multiplicar o seu comprimento, pela sua altura e por sua largura.
Comprimento: C
Altura: A
Largura: L
Volume: V
V=C.A.L
Pronto, está feita a equação.
Para caucular o volume devemos multiplicar o seu comprimento, pela sua altura e por sua largura.
Comprimento: C
Altura: A
Largura: L
Volume: V
V=C.A.L
Pronto, está feita a equação.
quinta-feira, 14 de maio de 2009
Operações com Polinômios
Adição:
Para somar dois ou mais polinômios você deve igualar os termos procurando simplificar a operação, ja que na maioria dos casos o coeficiente não é apenas numerico também possuirá uma parte literal.
Possuo dois polinômios:
A e B; presciso saber a soma dos dois, ou seja, A+B, sabendo que A = 7n+19+2y e B = 6n-17+3y
Então:
A+B = (7n+19+2y)+(6n-17+3y)
Nesse caso, devemos somar primeiro, cada um dos termos que possuem variáveis identicas. ex.: 7n+6n e 3y+2y, também devemos somar as partes que SÃO APENAS NUMÉRICAS E QUE NAO POSSUEM VARIÁVEL, assim como: 19+(-17) = 2.
Somando ficará:
A+B = 13n+5y+2
Para somar dois ou mais polinômios você deve igualar os termos procurando simplificar a operação, ja que na maioria dos casos o coeficiente não é apenas numerico também possuirá uma parte literal.
Possuo dois polinômios:
A e B; presciso saber a soma dos dois, ou seja, A+B, sabendo que A = 7n+19+2y e B = 6n-17+3y
Então:
A+B = (7n+19+2y)+(6n-17+3y)
Nesse caso, devemos somar primeiro, cada um dos termos que possuem variáveis identicas. ex.: 7n+6n e 3y+2y, também devemos somar as partes que SÃO APENAS NUMÉRICAS E QUE NAO POSSUEM VARIÁVEL, assim como: 19+(-17) = 2.
Somando ficará:
A+B = 13n+5y+2
quinta-feira, 30 de abril de 2009
O que é um Monômio? e Polinômio?
Monômio, meu caro amigo, é uma expressão algébrica formada por uma parte numérica e uma parte literal na qual não há operação de adição ou subtração entre elas.
3x é um monômio.
4y é um monômio.
Polinômio não tem uma definição específica, podemos encontrar várias definições diferentes como:
- Polinômio é uma expressão algébrica com todos os termos semelhantes reduzidos.
- Polinômio é um ou mais monômios separados por operações.
Existem polinômios de apenas um termo que são chamados de monômios, há outros que possuem dois ou mais termos, são os binômios, trinômios ou generalizados polinômios.
Exemplos de polinômios:
► -5xy é monômio, mas também considerado polinômio, assim podemos dividir os polinômios em monômios (apenas um monômio), binômio (dois monômios) e trinômio (três monômios).
► -5x + 3 é um polinômio e uma expressão algébrica.
Os polinômios são chamados conforme o seu grau. Para identificar o seu grau, basta observar o grau do maior monômio, esse será o grau do polinômio.
Com os polinômios podemos efetuar todas as operações: adição, subtração, divisão, multiplicação, potenciação.
3x é um monômio.
4y é um monômio.
Polinômio não tem uma definição específica, podemos encontrar várias definições diferentes como:
- Polinômio é uma expressão algébrica com todos os termos semelhantes reduzidos.
- Polinômio é um ou mais monômios separados por operações.
Existem polinômios de apenas um termo que são chamados de monômios, há outros que possuem dois ou mais termos, são os binômios, trinômios ou generalizados polinômios.
Exemplos de polinômios:
► -5xy é monômio, mas também considerado polinômio, assim podemos dividir os polinômios em monômios (apenas um monômio), binômio (dois monômios) e trinômio (três monômios).
► -5x + 3 é um polinômio e uma expressão algébrica.
Os polinômios são chamados conforme o seu grau. Para identificar o seu grau, basta observar o grau do maior monômio, esse será o grau do polinômio.
Com os polinômios podemos efetuar todas as operações: adição, subtração, divisão, multiplicação, potenciação.
quinta-feira, 23 de abril de 2009
Expressões Algébricas
EXPRESSÕES ALGÉBRICAS
Definição
As letras, na matemática, são usadas para representar números desconhecidos ou para generalizar propriedades e fórmulas da Geometria.
As expressões que apresentam letras, além de operações e números são denominadas de EXPRESSÕES ALGÉBRICAS e as letras são chamadas de variáveis.
Veja esta definição:
TODO NÚMERO NATURAL MULTIPLICADO PELO NÚMERO 1 É IGUAL A ELE MESMO
Assim, na matemática, essa propriedade pode ser escrita e representada da seguinte maneira:
x . 1 = x
Onde X representa um número natural qualquer podendo, por tanto, a sentença assumir quaisquer valores.
Exemplo para fixação de definição
a) Uma pessoa ganha R$ 30,00 por dia de trabalho. Para se efetuar o cálculo de quanto essa pessoa ganhará durante alguns dias de trabalho, é possível escrever a seguinte expressão algébrica:
30 . x
Onde X representa o número de dias trabalhados, que pode variar: 01 dia, 02 dias, 15 dias e etc.
Resolvendo então algumas sentenças do problema acima:
- Se a pessoa trabalhar 03 dias:
30 . 3 = R$ 90,00
- Se a pessoa trabalhar 15 dias:
30 . 15 = R$ 450,00
b) Um alimento tem o custo de R$ 5,00 a unidade. Para se efetuar o cálculo de quanto custaria levar uma maior quantidade deste alimento, é possível escrever a seguinte expressão algébrica:
R$ 5,00 . x
Onde X representa a quantidade de alimentos que se deseja levar, que pode ser: 01 unidade, 100 unidades e etc.
Resolvendo então algumas sentenças do exemplo acima:
- Se for comprado 12 unidade do alimento
R$ 5,00 x 12 = R$ 60,00
- Se for comprado 05 unidades do alimento
R$ 5,00 x 5 = R$ 25,00
Desta forma, é observado que a expressão algébrica nos permite efetuar os cálculos acima, por meio de variáveis.
Observe este exemplo sobre a área de um quadrado.
A expressão algébrica da área de um quadrado de X cm de lado é determinada elevando-se a medida do seu lado ao quadrado. Acompanhe:
Área: x²
Desta forma, é possível determinar a área de qualquer quadrado, substituindo a variável X pela medida do lado do quadrado.
Observações importantes sobre expressões algébricas
1) Nas expressões algébricas não é comum se escrever o sinal de multiplicação, observe:
3.x » se representa 3x
a.b » se representa ab
5.y » se representa 5y
2.x » se representa 2x
2) É possível ter expressões algébricas com mais de uma variável ou ainda sem variável.
4xy » expressão algébrica com duas variáveis: x e y
5a²bc²» expressão algébrica com três variáveis: a, b e c
35 » expressão algébrica sem variável
O que é valor numérico
Em expressões algébricas quando substituímos variáveis de uma sentença por números e efetuamos as devidas operações, o resultado encontrado é o valor numérico da expressão.
O valor numérico da expressão 4x + 3, para o valor de X = 4 é:
4x + 3 =
4.4 + 3 =
16 + 3 = 19
Levando esta solução para resolver problemas com retângulos, observe a sentença colocada abaixo:
Dimensões: a = 3 cm e b = 2 cm
Desta forma, o valor numérico da sentença ab é calculado:
a = 3
b = 2
3 x 2 = 6
Logo, a área correspondente do retângulo dado é 6 cm.
Monômios
As expressões algébricas que não representam as operações de adição e subtração entre os números e as variáveis, são denominadas de monômios.
Observe os exemplos:
6x, 4x, 5y, 7y
3x²y², 4x²y²
ab, 10, 12
A parte numérica de uma expressão algébrica chamada de monômios é denominada coeficiente e a outra parte da sentença formada por letras é chamada de parte literal.
Exemplos para fixação de conteúdo
De acordo com a definição sobre monômios, vamos destacar nas sentenças abaixo a parte literal e o coeficiente:
- 6x
Coeficiente: 6
Parte Literal: x
- 10y
Coeficiente: 10
Parte Literal: y
- 4x²y²
Coeficiente: 4
Parte Literal: x²y²
- 5xy²
Coeficiente: 5
Parte Literal: xy²
- bc
Coeficiente: 1 (bc é igual 1bc)
Parte Literal: bc
- 15
Coeficiente: 15
Parte Literal: Não existe
Operações matemáticas com monômios
Dois ou mais monômios que possuem a mesma parte literal e também coeficientes diferentes são denominados de monômios parecidos ou monômios semelhantes.
Para se efetuar operações matemáticas de subtração e soma eles devem ser semelhantes, ou seja, possuir a mesma parte literal e também mesmo coeficientes. Caso isto não ocorra, a adição e a subtração serão apenas indicadas, porém não poderá ser efetuado nenhum cálculo.
Exemplos para fixação de conteúdo
De acordo com a definição fornecida acima, vamos ver alguns exemplos com cálculos envolvendo monômios.
a) 5xy + 12xy + 3xy
(5 + 12 + 3)xy
20xy
b) 4xy – 2xy + 7xy
(4 – 2 + 7)xy
9xy
c) 4x – 2xy + 3xy
(Operação não é possível porque os monômios não são semelhantes)
Definição
As letras, na matemática, são usadas para representar números desconhecidos ou para generalizar propriedades e fórmulas da Geometria.
As expressões que apresentam letras, além de operações e números são denominadas de EXPRESSÕES ALGÉBRICAS e as letras são chamadas de variáveis.
Veja esta definição:
TODO NÚMERO NATURAL MULTIPLICADO PELO NÚMERO 1 É IGUAL A ELE MESMO
Assim, na matemática, essa propriedade pode ser escrita e representada da seguinte maneira:
x . 1 = x
Onde X representa um número natural qualquer podendo, por tanto, a sentença assumir quaisquer valores.
Exemplo para fixação de definição
a) Uma pessoa ganha R$ 30,00 por dia de trabalho. Para se efetuar o cálculo de quanto essa pessoa ganhará durante alguns dias de trabalho, é possível escrever a seguinte expressão algébrica:
30 . x
Onde X representa o número de dias trabalhados, que pode variar: 01 dia, 02 dias, 15 dias e etc.
Resolvendo então algumas sentenças do problema acima:
- Se a pessoa trabalhar 03 dias:
30 . 3 = R$ 90,00
- Se a pessoa trabalhar 15 dias:
30 . 15 = R$ 450,00
b) Um alimento tem o custo de R$ 5,00 a unidade. Para se efetuar o cálculo de quanto custaria levar uma maior quantidade deste alimento, é possível escrever a seguinte expressão algébrica:
R$ 5,00 . x
Onde X representa a quantidade de alimentos que se deseja levar, que pode ser: 01 unidade, 100 unidades e etc.
Resolvendo então algumas sentenças do exemplo acima:
- Se for comprado 12 unidade do alimento
R$ 5,00 x 12 = R$ 60,00
- Se for comprado 05 unidades do alimento
R$ 5,00 x 5 = R$ 25,00
Desta forma, é observado que a expressão algébrica nos permite efetuar os cálculos acima, por meio de variáveis.
Observe este exemplo sobre a área de um quadrado.
A expressão algébrica da área de um quadrado de X cm de lado é determinada elevando-se a medida do seu lado ao quadrado. Acompanhe:
Área: x²
Desta forma, é possível determinar a área de qualquer quadrado, substituindo a variável X pela medida do lado do quadrado.
Observações importantes sobre expressões algébricas
1) Nas expressões algébricas não é comum se escrever o sinal de multiplicação, observe:
3.x » se representa 3x
a.b » se representa ab
5.y » se representa 5y
2.x » se representa 2x
2) É possível ter expressões algébricas com mais de uma variável ou ainda sem variável.
4xy » expressão algébrica com duas variáveis: x e y
5a²bc²» expressão algébrica com três variáveis: a, b e c
35 » expressão algébrica sem variável
O que é valor numérico
Em expressões algébricas quando substituímos variáveis de uma sentença por números e efetuamos as devidas operações, o resultado encontrado é o valor numérico da expressão.
O valor numérico da expressão 4x + 3, para o valor de X = 4 é:
4x + 3 =
4.4 + 3 =
16 + 3 = 19
Levando esta solução para resolver problemas com retângulos, observe a sentença colocada abaixo:
Dimensões: a = 3 cm e b = 2 cm
Desta forma, o valor numérico da sentença ab é calculado:
a = 3
b = 2
3 x 2 = 6
Logo, a área correspondente do retângulo dado é 6 cm.
Monômios
As expressões algébricas que não representam as operações de adição e subtração entre os números e as variáveis, são denominadas de monômios.
Observe os exemplos:
6x, 4x, 5y, 7y
3x²y², 4x²y²
ab, 10, 12
A parte numérica de uma expressão algébrica chamada de monômios é denominada coeficiente e a outra parte da sentença formada por letras é chamada de parte literal.
Exemplos para fixação de conteúdo
De acordo com a definição sobre monômios, vamos destacar nas sentenças abaixo a parte literal e o coeficiente:
- 6x
Coeficiente: 6
Parte Literal: x
- 10y
Coeficiente: 10
Parte Literal: y
- 4x²y²
Coeficiente: 4
Parte Literal: x²y²
- 5xy²
Coeficiente: 5
Parte Literal: xy²
- bc
Coeficiente: 1 (bc é igual 1bc)
Parte Literal: bc
- 15
Coeficiente: 15
Parte Literal: Não existe
Operações matemáticas com monômios
Dois ou mais monômios que possuem a mesma parte literal e também coeficientes diferentes são denominados de monômios parecidos ou monômios semelhantes.
Para se efetuar operações matemáticas de subtração e soma eles devem ser semelhantes, ou seja, possuir a mesma parte literal e também mesmo coeficientes. Caso isto não ocorra, a adição e a subtração serão apenas indicadas, porém não poderá ser efetuado nenhum cálculo.
Exemplos para fixação de conteúdo
De acordo com a definição fornecida acima, vamos ver alguns exemplos com cálculos envolvendo monômios.
a) 5xy + 12xy + 3xy
(5 + 12 + 3)xy
20xy
b) 4xy – 2xy + 7xy
(4 – 2 + 7)xy
9xy
c) 4x – 2xy + 3xy
(Operação não é possível porque os monômios não são semelhantes)
Potências
POTÊNCIAS
* Definição
Dado um certo número real qualquer, e um número n, inteiro e positivo, é definido in = potência de base (i) e com expoente (n) como sendo o produto de n fatores iguais a (i).
Exemplos de fixação da definição:
Potência = 23
2 x 2 x 2 = ( 03 fatores) = 8
Potência = 35
3 x 3 x 3 x 3 x 3 = (05 fatores) = 243
Notação: 23 = 8
2 - BASE
3 - EXPOENTE
8 - POTÊNCIA
Notação: 35 = 243
3 - BASE
5 - EXPOENTE
243 - POTÊNCIA
Alguns casos particulares:
1) Expoente igual a um (1)
(1/2)1 = 1/2
51 = 5
31 = 3
2) Expoente igual à zero (0)
50 = 1
60 = 1
70 = 1
Por convenção, resolveu-se que toda número elevado ao número zero, o resultado será igual a 1.
Mais Exemplos de fixação da definição:
1) 53 = 5 x 5 x 5 = 125
2) 40 = 1
3) 100 = 1
4) 201 = 20
* Propriedades de Potências
- Divisão de potência de mesma base
Na operação de divisão de potências de mesma base, é conservada a base comum e subtraem-se os expoentes conforme a ordem o qual eles aparecem no problema.
Exemplos de fixação:
1) 24 ÷ 2 = 24-1 = 23
2) 35 ÷ 32 = 35-2 = 32
3) 46 ÷ 43 = 46-3 = 43
Temos então: Im ÷ In = Im-n , I#0
- Produto de potência de mesma base
Na operação de multiplicação entre potências de mesma base, é conservada a base comum e somam-se os expoentes em qualquer ordem dada no problema.
Exemplos de fixação:
1) 24 x 2 = 24+1 = 25
2) 35 x 32 = 35+2 = 37
3) 46 x 43 = 46+3 = 49
Temos então: Im x In = Im+n
- Potência de Potência
Podemos elevar uma potência a outra potência. Para se efetuar este cálculo conserva-se a base comum e multiplicam-se os expoentes respectivos.
Exemplos de fixação:
1) (23)4 = 212 , pois = 23 x 23 x 23 x 23
2) (32)3 = 36 , pois = 32 x 32 x 32
3) (42)5 = 410 , pois = 42 x 42 x 42 x 42 x 42
Temos então: (In)m = Inxm
- Potência de um produto
Para se efetuar esta operação de potência de um produto, podemos elevar cada fator a esta potência.
Exemplos de fixação:
1) (b5ya3 )4 = b20y4a12
2) (c2d2e5 )2 = c4d4e10
3) (d3a4 )3 = d9a12
Temos então: (I.T)m = I m x T m
- Potência com expoente negativo
Toda e qualquer potência que tenha expoente negativo é equivalente a uma fração o qual o numerador é a unidade positiva e o denominador é a mesma potência, porém apresentando o expoente positivo.
Exemplos de fixação:
1) 2-4 = 1/24 = 1/16
2) 3-3 = 1/33 = 1/27
3) 4-2 = 1/42 = 1/16
Temos então: (I)-m = 1/I m I#0
- Potência de fração
Para se efetuar o cálculo deste tipo de fração, eleva-se o numerador e denominador, respectivamente, a esta potência.
1) (a/b)4 = a4/b4 = b#0
2) (a2 /b4)3 = a6/b12 = b#0
3) (a3 /b2)3 = a9/b6 = b#0
Temos então: (a/b)m = am/bm b #0
- Potência de 10
Todas as potências de 10 têm a função de facilitar o cálculo de várias expressões. Para isto guarde bem estas técnicas :
1) Para se elevar 10n (N>0), basta somente escrever a quantidade de zeros da potência a direito do número 1.
Exemplos de fixação:
a) 104 = 10000
b) 106 = 1000000
c) 107 = 10000000
2) Para se elevar 10-n (N>0), basta somente escrever a quantidade de zeros da potência a esquerda do número 1, colocando a vírgula depois do primeiro zero que se escreveu.
Exemplos de fixação:
a) 10-4 = 0,0001
b) 10-6 = 0,000001
c) 10-7 = 0,0000001
3) Decompondo números em potências de 10
Exemplos de fixação (números maiores que 1):
a) 300 = 3.100 = 3.102
b) 7000 = 7.1000 = 7.103
c) 10.000 = 1.10000 = 1.104
Exemplos de fixação (números menores que 1):
a) 0,004 = 4.0,001 = 4.10-3
b) 0,0008 = 8.0,0001 = 8.10-4
c) 0,00009 = 9.0,00001 = 9.10-5
- Potência de números relativos
a) Caso o expoente seja par o resultado dará sempre positivo.
Veja: (+2)2 = 4 / / (-2)4 = 16
b) Caso o expoente seja impar, o resultado trará sempre o sinal da base da potência.
Veja: (+3)3 = 27 / / (-3)3 = -27
Observação importante: -22 # (-2) 2 , pois -22 = -4 e (-2) 2 = 4. A diferença está que na primeira potência apenas o número 2 está elevado ao quadrado, enquanto que na segunda o sinal e o número 2 estão elevados ao quadrado, tornando o resultado, então, positivo, conforme colocado.
* Definição
Dado um certo número real qualquer, e um número n, inteiro e positivo, é definido in = potência de base (i) e com expoente (n) como sendo o produto de n fatores iguais a (i).
Exemplos de fixação da definição:
Potência = 23
2 x 2 x 2 = ( 03 fatores) = 8
Potência = 35
3 x 3 x 3 x 3 x 3 = (05 fatores) = 243
Notação: 23 = 8
2 - BASE
3 - EXPOENTE
8 - POTÊNCIA
Notação: 35 = 243
3 - BASE
5 - EXPOENTE
243 - POTÊNCIA
Alguns casos particulares:
1) Expoente igual a um (1)
(1/2)1 = 1/2
51 = 5
31 = 3
2) Expoente igual à zero (0)
50 = 1
60 = 1
70 = 1
Por convenção, resolveu-se que toda número elevado ao número zero, o resultado será igual a 1.
Mais Exemplos de fixação da definição:
1) 53 = 5 x 5 x 5 = 125
2) 40 = 1
3) 100 = 1
4) 201 = 20
* Propriedades de Potências
- Divisão de potência de mesma base
Na operação de divisão de potências de mesma base, é conservada a base comum e subtraem-se os expoentes conforme a ordem o qual eles aparecem no problema.
Exemplos de fixação:
1) 24 ÷ 2 = 24-1 = 23
2) 35 ÷ 32 = 35-2 = 32
3) 46 ÷ 43 = 46-3 = 43
Temos então: Im ÷ In = Im-n , I#0
- Produto de potência de mesma base
Na operação de multiplicação entre potências de mesma base, é conservada a base comum e somam-se os expoentes em qualquer ordem dada no problema.
Exemplos de fixação:
1) 24 x 2 = 24+1 = 25
2) 35 x 32 = 35+2 = 37
3) 46 x 43 = 46+3 = 49
Temos então: Im x In = Im+n
- Potência de Potência
Podemos elevar uma potência a outra potência. Para se efetuar este cálculo conserva-se a base comum e multiplicam-se os expoentes respectivos.
Exemplos de fixação:
1) (23)4 = 212 , pois = 23 x 23 x 23 x 23
2) (32)3 = 36 , pois = 32 x 32 x 32
3) (42)5 = 410 , pois = 42 x 42 x 42 x 42 x 42
Temos então: (In)m = Inxm
- Potência de um produto
Para se efetuar esta operação de potência de um produto, podemos elevar cada fator a esta potência.
Exemplos de fixação:
1) (b5ya3 )4 = b20y4a12
2) (c2d2e5 )2 = c4d4e10
3) (d3a4 )3 = d9a12
Temos então: (I.T)m = I m x T m
- Potência com expoente negativo
Toda e qualquer potência que tenha expoente negativo é equivalente a uma fração o qual o numerador é a unidade positiva e o denominador é a mesma potência, porém apresentando o expoente positivo.
Exemplos de fixação:
1) 2-4 = 1/24 = 1/16
2) 3-3 = 1/33 = 1/27
3) 4-2 = 1/42 = 1/16
Temos então: (I)-m = 1/I m I#0
- Potência de fração
Para se efetuar o cálculo deste tipo de fração, eleva-se o numerador e denominador, respectivamente, a esta potência.
1) (a/b)4 = a4/b4 = b#0
2) (a2 /b4)3 = a6/b12 = b#0
3) (a3 /b2)3 = a9/b6 = b#0
Temos então: (a/b)m = am/bm b #0
- Potência de 10
Todas as potências de 10 têm a função de facilitar o cálculo de várias expressões. Para isto guarde bem estas técnicas :
1) Para se elevar 10n (N>0), basta somente escrever a quantidade de zeros da potência a direito do número 1.
Exemplos de fixação:
a) 104 = 10000
b) 106 = 1000000
c) 107 = 10000000
2) Para se elevar 10-n (N>0), basta somente escrever a quantidade de zeros da potência a esquerda do número 1, colocando a vírgula depois do primeiro zero que se escreveu.
Exemplos de fixação:
a) 10-4 = 0,0001
b) 10-6 = 0,000001
c) 10-7 = 0,0000001
3) Decompondo números em potências de 10
Exemplos de fixação (números maiores que 1):
a) 300 = 3.100 = 3.102
b) 7000 = 7.1000 = 7.103
c) 10.000 = 1.10000 = 1.104
Exemplos de fixação (números menores que 1):
a) 0,004 = 4.0,001 = 4.10-3
b) 0,0008 = 8.0,0001 = 8.10-4
c) 0,00009 = 9.0,00001 = 9.10-5
- Potência de números relativos
a) Caso o expoente seja par o resultado dará sempre positivo.
Veja: (+2)2 = 4 / / (-2)4 = 16
b) Caso o expoente seja impar, o resultado trará sempre o sinal da base da potência.
Veja: (+3)3 = 27 / / (-3)3 = -27
Observação importante: -22 # (-2) 2 , pois -22 = -4 e (-2) 2 = 4. A diferença está que na primeira potência apenas o número 2 está elevado ao quadrado, enquanto que na segunda o sinal e o número 2 estão elevados ao quadrado, tornando o resultado, então, positivo, conforme colocado.
quinta-feira, 2 de abril de 2009
Notação Científica
Geralmente usa-se o seguinte formato:
N X 10x onde N= número maior do que 1 mas inferior a 10
e x= o exponente de 10.
Escrever um número na notação exponencial (notação científica) tem muitas vantagens:
Para os números muito grandes ou muito pequenos poderem ser escritos de forma mais abreviada.
Na utilização dos computadores ou máquinas de calcular esta notação tem um uso regular.
Tornam os cálculos muito mais rápidos e fáceis.
Números maiores que 10
Localizada a vírgula desloca-se esta para a esquerda por forma a ficar um algarismo não nulo à esquerda.
Esse inteiro será o N (atrás referido) da expressão correspondente à notação científica.
Conta-se o número de casas que a vírgula andou no ponto nº 1, esse será o expoente de 10.
Assim obtemos o número escrito sob a forma : N X 10x.
Vamos ao primeiro exemplo que podes seguir passo a passo
Seja o número 23419 :
na notação científica como se escreve?
Vamos deslocar a vírgula 4 casas para a esquerda e fica:
2.3419
O expoente encontrado será 4
Escreve-se agora o produto:
Ou seja: 2.3419 X 10 4
Como fazer quando os números são menores que um?
Vamos seguir exactamente os mesmos passos do item anterior só que a vírgula vai deslocar.se para a DIREITA. O número de posições ou casas que a vírgula se deslocou para a direita será o nosso -x (expoente negativo de 10)
Convém recordar que uma potência de expoente negativo pode ser escrita com o uso de um expoente positivo. Exemplo::
10-5 pode ser reescrito como 1/ 105.
Vamos escrever agora um número em notação científica. Seja:
0.000436
Primeiro vamos deslocar a vírgula por forma a termos uma parte inteira não nula e menor que 10:
Teremos : 4.36
A vírgula deslocou-se para a direita quatro casas. Então o expoente de 10 será -4
E a expressão final será: 4.36 X 10-4
E se o número está entre 1 e 10?
(Este é o caso com menor interesse)
Neste caso não é necessário mover a vírgula basta só recordar que 100 =1 (como todas as potências de expoente zero) Então vamos ver o exemplo seguinte:
7.92 pode ser escrito como: 7.92 X 1 = 7.92X 100
I
Escreve agora os números dados com a notação científica:
123,8763
1236,840.
4.22
0.000000000000211
0.000238
9.10
Uma das vantagens desta notação, que foi mencionada no início, era a facilidade de operar com esses números de uma forma mais fácil do que com os seus equivalentes numéricos . Vamos ver como multiplicar num caso desses: De uma forma geral tem-se:
(N X 10x) (M X 10y) = (N X M) X 10x+y
Primeiro multiplica-se N por M .
Depois efectua-se a multiplicação das potências (soma-se os expoentes).
Finalmente seguem-se as regras atrás expostas.
Por exemplo:
(3 X 104) X (102)
Em primeiro lugar : 3 X 1=3
Segue-se (104) (102) = 104+2 = 106
Neste caso o resultado seria 3 X 106
Outro exemplo :
(4 X 103) (2 X 10-4)
Primeiro 4 X 2 = 8
Depois (103) (10-4) = 103+(-4) = 103-4 = 10-1
Resultado 8 X 10-1
II
Agora outros exemplos para tu fazeres:
(3 X 105) (3 X 106) = ?
(2 X 107) (3 X 10-9) = ?
(4 X 10-6) (4 X 10-4) = ?
Convém ainda veres o que fazer em casos como este: 13,5 X 108 , e isto acontece muitas vezes como resultado de uma operação. Claro que é simples:
Por exemplo: 13,5 X 108
Basta ajustar como anteriormente a colocação da vírgula: 1,35 X 101X 108 = 1.35 X 109
O mesmo para casos como 0.03X104 (onde o N é um número igual a 0 )
Vê este exemplo : 0.0078 X 105 =7.8 X 10(-3)X 105 = 7.8 X 105-3 = 7.8 X 102
Foi necessário mover a vírgula 3 casas:
7.8 X 105+(-3) = 7.8 X 105-3 = 7.8 X 102
Divisão de dois números em notação científica
O caso geral pode ser expresso por :
N X 10x / M X 10y = N/M X 10x-y
Claro está que depois de efectuada a divisão de N por M há que, se o resultado precisar, utilizar os procedimentos atrás mencionados. Cuidado com os sinais ao subtrair os expoentes !
Eis um exemplo : 6 X 105 : 2 X 102 =
Fazer a divisão de N por M ou seja 6/2 = 3
Subtarir os expoentes, pois 105 : 102 = 105-2 = 103
Apresentar o resultado final : 3 x 103
III
Apresenta os resultados das operações indicadas na notação científica
3.45 X 108 / 6.74 X 10-2 = ?
6.7 X 107 / 8.6 X 103 = ?
4.7 X 10-2 / 5.7 X 10-6 = ?
Adição e Subtracção de números em notação científica
Nos casos mais simples onde os expoentes de 10 são iguais , basta pôr em evidência a potência de 10 que é comum:
(N X 10x) + (M X 10x) = (N + M) X 10x
ou
(N X 10y) - (M X 10y) = (N-M) X 10y
Sempre com o cuidado já atrás recomendado : verificar se o resultado de N-M ou N+M não precisa de ser também trabalhado
Mas nem sempre os expoentes dos números são iguais. Então há que transformar os números por forma que isso aconteça .
Exemplo :(2.3 X 10-2) + (3.1 X 10-3)
Vamos então transformar o primeiro número (podiamos optar por o fazer com o segundo)
2.3 X 10-2 =23. 10(-1) X 10-2 = 23. X 10-3
Agora já a operação é simples: (23. X 10-3) + (3.1 X 10-3) = (23. + 3.1) X 10-3 = 26.1 X 10-3
Mas atenção: 26.1 é maior que 10 logo : 26.1 X 10-3 =2.61 X 10 X 10-3 ou seja 2.61 X 10-2
Outro exemplo:
(4.2 X 104) - (2.7 X 102) =
Agora, para variar, vamos ajustar o 2º número
2.7 X 102 fica 0 .027 X 102+2 = 0.027 X 104
E a operação pode escrever-se: (4.2 X 104) - (0.027 X 104) = (4.2 - 0.027) X 104 = 4.173 X 104
IV
Efectua:
(8.41 X 103) + (9.71 X 104) = ?
(5.11 X 102) - (4.2 X 102) = ?
(8.2 X 102) + (4.0 X 103) = ?
(6.3 X 10-2) - (2.1 X 10-1) = ?
Nota final: Quer nos computadores, quer nas máquinas de calcular ou mesmo na escrita normal o 10 da base é substituido por E . Assim : (5.11 X 102) - (4.2 X 10-3) aparece assim : (5.11 X E2) - (4.2 X E -3) ou mais simples : (5.11 .E2) - (4.2 .E-3) .
Nalguns casos o próprio E é omitido
N X 10x onde N= número maior do que 1 mas inferior a 10
e x= o exponente de 10.
Escrever um número na notação exponencial (notação científica) tem muitas vantagens:
Para os números muito grandes ou muito pequenos poderem ser escritos de forma mais abreviada.
Na utilização dos computadores ou máquinas de calcular esta notação tem um uso regular.
Tornam os cálculos muito mais rápidos e fáceis.
Números maiores que 10
Localizada a vírgula desloca-se esta para a esquerda por forma a ficar um algarismo não nulo à esquerda.
Esse inteiro será o N (atrás referido) da expressão correspondente à notação científica.
Conta-se o número de casas que a vírgula andou no ponto nº 1, esse será o expoente de 10.
Assim obtemos o número escrito sob a forma : N X 10x.
Vamos ao primeiro exemplo que podes seguir passo a passo
Seja o número 23419 :
na notação científica como se escreve?
Vamos deslocar a vírgula 4 casas para a esquerda e fica:
2.3419
O expoente encontrado será 4
Escreve-se agora o produto:
Ou seja: 2.3419 X 10 4
Como fazer quando os números são menores que um?
Vamos seguir exactamente os mesmos passos do item anterior só que a vírgula vai deslocar.se para a DIREITA. O número de posições ou casas que a vírgula se deslocou para a direita será o nosso -x (expoente negativo de 10)
Convém recordar que uma potência de expoente negativo pode ser escrita com o uso de um expoente positivo. Exemplo::
10-5 pode ser reescrito como 1/ 105.
Vamos escrever agora um número em notação científica. Seja:
0.000436
Primeiro vamos deslocar a vírgula por forma a termos uma parte inteira não nula e menor que 10:
Teremos : 4.36
A vírgula deslocou-se para a direita quatro casas. Então o expoente de 10 será -4
E a expressão final será: 4.36 X 10-4
E se o número está entre 1 e 10?
(Este é o caso com menor interesse)
Neste caso não é necessário mover a vírgula basta só recordar que 100 =1 (como todas as potências de expoente zero) Então vamos ver o exemplo seguinte:
7.92 pode ser escrito como: 7.92 X 1 = 7.92X 100
I
Escreve agora os números dados com a notação científica:
123,8763
1236,840.
4.22
0.000000000000211
0.000238
9.10
Uma das vantagens desta notação, que foi mencionada no início, era a facilidade de operar com esses números de uma forma mais fácil do que com os seus equivalentes numéricos . Vamos ver como multiplicar num caso desses: De uma forma geral tem-se:
(N X 10x) (M X 10y) = (N X M) X 10x+y
Primeiro multiplica-se N por M .
Depois efectua-se a multiplicação das potências (soma-se os expoentes).
Finalmente seguem-se as regras atrás expostas.
Por exemplo:
(3 X 104) X (102)
Em primeiro lugar : 3 X 1=3
Segue-se (104) (102) = 104+2 = 106
Neste caso o resultado seria 3 X 106
Outro exemplo :
(4 X 103) (2 X 10-4)
Primeiro 4 X 2 = 8
Depois (103) (10-4) = 103+(-4) = 103-4 = 10-1
Resultado 8 X 10-1
II
Agora outros exemplos para tu fazeres:
(3 X 105) (3 X 106) = ?
(2 X 107) (3 X 10-9) = ?
(4 X 10-6) (4 X 10-4) = ?
Convém ainda veres o que fazer em casos como este: 13,5 X 108 , e isto acontece muitas vezes como resultado de uma operação. Claro que é simples:
Por exemplo: 13,5 X 108
Basta ajustar como anteriormente a colocação da vírgula: 1,35 X 101X 108 = 1.35 X 109
O mesmo para casos como 0.03X104 (onde o N é um número igual a 0 )
Vê este exemplo : 0.0078 X 105 =7.8 X 10(-3)X 105 = 7.8 X 105-3 = 7.8 X 102
Foi necessário mover a vírgula 3 casas:
7.8 X 105+(-3) = 7.8 X 105-3 = 7.8 X 102
Divisão de dois números em notação científica
O caso geral pode ser expresso por :
N X 10x / M X 10y = N/M X 10x-y
Claro está que depois de efectuada a divisão de N por M há que, se o resultado precisar, utilizar os procedimentos atrás mencionados. Cuidado com os sinais ao subtrair os expoentes !
Eis um exemplo : 6 X 105 : 2 X 102 =
Fazer a divisão de N por M ou seja 6/2 = 3
Subtarir os expoentes, pois 105 : 102 = 105-2 = 103
Apresentar o resultado final : 3 x 103
III
Apresenta os resultados das operações indicadas na notação científica
3.45 X 108 / 6.74 X 10-2 = ?
6.7 X 107 / 8.6 X 103 = ?
4.7 X 10-2 / 5.7 X 10-6 = ?
Adição e Subtracção de números em notação científica
Nos casos mais simples onde os expoentes de 10 são iguais , basta pôr em evidência a potência de 10 que é comum:
(N X 10x) + (M X 10x) = (N + M) X 10x
ou
(N X 10y) - (M X 10y) = (N-M) X 10y
Sempre com o cuidado já atrás recomendado : verificar se o resultado de N-M ou N+M não precisa de ser também trabalhado
Mas nem sempre os expoentes dos números são iguais. Então há que transformar os números por forma que isso aconteça .
Exemplo :(2.3 X 10-2) + (3.1 X 10-3)
Vamos então transformar o primeiro número (podiamos optar por o fazer com o segundo)
2.3 X 10-2 =23. 10(-1) X 10-2 = 23. X 10-3
Agora já a operação é simples: (23. X 10-3) + (3.1 X 10-3) = (23. + 3.1) X 10-3 = 26.1 X 10-3
Mas atenção: 26.1 é maior que 10 logo : 26.1 X 10-3 =2.61 X 10 X 10-3 ou seja 2.61 X 10-2
Outro exemplo:
(4.2 X 104) - (2.7 X 102) =
Agora, para variar, vamos ajustar o 2º número
2.7 X 102 fica 0 .027 X 102+2 = 0.027 X 104
E a operação pode escrever-se: (4.2 X 104) - (0.027 X 104) = (4.2 - 0.027) X 104 = 4.173 X 104
IV
Efectua:
(8.41 X 103) + (9.71 X 104) = ?
(5.11 X 102) - (4.2 X 102) = ?
(8.2 X 102) + (4.0 X 103) = ?
(6.3 X 10-2) - (2.1 X 10-1) = ?
Nota final: Quer nos computadores, quer nas máquinas de calcular ou mesmo na escrita normal o 10 da base é substituido por E . Assim : (5.11 X 102) - (4.2 X 10-3) aparece assim : (5.11 X E2) - (4.2 X E -3) ou mais simples : (5.11 .E2) - (4.2 .E-3) .
Nalguns casos o próprio E é omitido
quinta-feira, 26 de fevereiro de 2009
Tirando a Fração Geratriz
Dízimas periódicas simples
a) 0,2222...
Período: 2
Coloca-se o período no numerador da fração e, para cada algarismo dele, coloca-se um algarismo 9 no denominador.


Nesse caso, temos uma dízima simples e a parte inteira diferente de zero.Uma estratégia é separar parte inteira e parte decimal:

Dízimas periódicas compostas
a) 0,27777...
Aqui, a dica é um pouco diferente: para cada algarismo do período ainda se coloca um algarismo 9 no denominador. Mas, agora, para cada algarismo do antiperíodo se coloca um algarismo zero, também no denominador.
No caso do numerador, faz-se a seguinte conta: (parte inteira com antiperíodo e período) - (parte inteira com antiperíodo)
Assim:
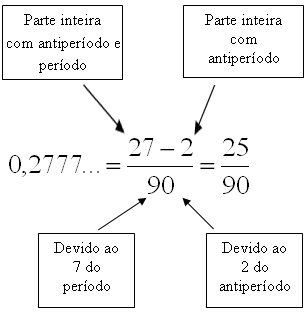
b) 1,64444...

c) 21,308888... (o período tem 1 algarismo e o antiperíodo tem 2 algarismos)

d) 2,4732121212... (o período tem 2 algarismos e o antiperíodo tem 3 algarismos)

Por que dá certo?
Veja a explicação na forma como geralmente se aprende a achar a fração geratriz na escola:
Chama-se a fração geratriz de x:

a) 0,2222...
Período: 2
Coloca-se o período no numerador da fração e, para cada algarismo dele, coloca-se um algarismo 9 no denominador.


Nesse caso, temos uma dízima simples e a parte inteira diferente de zero.Uma estratégia é separar parte inteira e parte decimal:

Dízimas periódicas compostas
a) 0,27777...
Aqui, a dica é um pouco diferente: para cada algarismo do período ainda se coloca um algarismo 9 no denominador. Mas, agora, para cada algarismo do antiperíodo se coloca um algarismo zero, também no denominador.
No caso do numerador, faz-se a seguinte conta: (parte inteira com antiperíodo e período) - (parte inteira com antiperíodo)
Assim:

b) 1,64444...

c) 21,308888... (o período tem 1 algarismo e o antiperíodo tem 2 algarismos)

d) 2,4732121212... (o período tem 2 algarismos e o antiperíodo tem 3 algarismos)

Por que dá certo?
Veja a explicação na forma como geralmente se aprende a achar a fração geratriz na escola:
Chama-se a fração geratriz de x:

Para achar o valor de x, encontram-se múltiplos dele com apenas o período na parte decimal
E subtraem-se as duas igualdades
Assim, cria-se uma equação e elimina-se a parte infinita dos números envolvidos, achando-se a fração geratriz.Note que, no método mais prático, a conta sugerida é a mesma que aparece na equação: 164 - 16, e o denominador fica exatamente com os mesmos algarismos.No caso do exemplo D, deve-se multiplicar x por números ainda maiores, para se achar a mesma parte decimal nos dois números a serem subtraídos:
sábado, 14 de fevereiro de 2009
quinta-feira, 12 de fevereiro de 2009
Classificação dos números.

Números Naturais
Naturais é a forma mais simples de classificassão de números. São eles o : 0, 1, 2, 3...
A imagem a esquerda é o símbolo de como os números naturais são representados matemáticamente.
Números Inteiros
Inteiros é a segunda fora mais simples de números, os números Naturais sempre participaram dos Inteiros: ...-1, -2, -3, 0, 1, 2, 3...
Ainda nao econtramos a imagem que representa os números inteiros matemáticamente.
Números Racionais
Racionais é um forma bem coplexa de números nela estão os números: fracionários, décimais, inteiros, racionais, dízimas periódicas e raízes exatas.Ainda nao econtramos a imagem que representa os números racionais matemáticamente.
Números Irracionais
Irracionais é um pequeno grupo de números, nele estão apenas: raízes não exatas e dízimas não periódicas.
Números Irracionais
Irracionais é um pequeno grupo de números, nele estão apenas: raízes não exatas e dízimas não periódicas.
Ainda nao econtramos a imagem que representa os números irracionais matemáticamente.
Números Reais
Numerais Reais é o último e maior grupo de números, nele estão: fracionários, décimais, inteiros, racionais, dízimas periódicas, raízes exatas, raízes não exatas e dízimas não periódicas. Resumindo: estão todos os números (racionais e irracionais)
Números Reais
Numerais Reais é o último e maior grupo de números, nele estão: fracionários, décimais, inteiros, racionais, dízimas periódicas, raízes exatas, raízes não exatas e dízimas não periódicas. Resumindo: estão todos os números (racionais e irracionais)
Assinar:
Postagens (Atom)




